![]()
Economia e Energia
Nº 106, janeiro a junho de 2020
ISSN 1518-2932 Disponível em: http://ecen.com
(números anteriores) http://ecen.com
ACOMPANHAMENTO E PROJEÇÃO DE ÓBITOS PELA COVID NO BRASIL
Redação Preliminar em Discussão E&E 106
Palavra do Editor
Razões para a divulgação desse Acompanhamento
Um conhecimento só é realmente útil quando possibilita uma “previsão” do futuro.
Prever o futuro no curto e médio prazo é uma tarefa ingrata porque os pretensos profetas serão punidos também no curto e médio prazo.
Cientes desse risco, resolvemos, mesmo assim, ir divulgando os resultados parciais de nossas projeções e questões na esperança que eles possam ser úteis.
Na realidade, como não se sabe o comportamento que será adotado por governos e cidadãos quanto ao isolamento social, não podemos ter uma ideia precisa do que acontecerá. O que a metodologia realmente fornece é uma ideia para onde estamos indo. Para onde realmente vamos é uma questão onde todos somos os protagonistas, conscientes ou não disto.
Ou seja, os autores deste trabalho já temos a desculpa padrão para nossas prováveis falhas.
Acreditamos que o exame dos dados por diferentes ângulos, mesmo por pessoas treinadas no uso das estatísticas, mas sem conhecimento específico do problema médicos, pode ser útil aos especialistas e a população interessada para compreender as possibilidades e os riscos envolvidos.
Estamos apresentando, nessa versão preliminar, os resultados comentados para o Rio de Janeiro e Brasil. Temos os mesmos dados disponíveis para as 5 Macrorregiões e para os estados. Nosso objetivo é de irmos aprofundando e corrigindo dados e observações ao longo da pandemia. Estamos naturalmente abertos a colaborações externas e ao debate,
Carlos Feu Alvim
Texto e dados em discussão, redação preliminar de 12/06/2020
COVID 19
Abordagem logística da propagação do Novo Coronavirus
Carlos Feu Alvim, Olga Mafra e José Israel Vargas
O tratamento logístico foi aplicado por Cesare Marchetti[1] a inúmeros sistemas sociais e econômicos e tecnológicos. No Brasil, o professor José Israel Vargas o aplicou também a diversos sistemas, com ênfase em casos brasileiros.
Aqui mesmo, já aplicamos esse ajuste para vários casos e o assunto já foi tratado no número zero dessa revista,[2] em artigo de Omar Campos Ferreira, e uma visão completa sobre a metodologia está no exemplar de número 45 da E&E, em artigo de José Israel Vargas “Prospectiva Tecnológica, Previsão com um Simples Modelo Matemático”[3].
A metodologia, que nasceu na análise de Volterra e Lotka de sistemas de competição biológica, pode ser aplicada à Covid 19 que está se colocando como a maior pandemia desde a gripe espanhola, ocorrida há praticamente um século (1918 a 1920).
Fundamentalmente, essa metodologia se baseia em um modelo no qual a taxa de infecção em uma população depende do número de infectados N e do número dos que restam a infectar (N*-N) sendo N* o número final de atingidos, denominado de nicho. Matematicamente isso se traduz na equação na qual, ao longo do tempo o número de contaminados será proporcional ao produto de um termo crescente N e outro decrescente
N*-N.
T = dN/dt = a.N.(N*-N) ou
T = a.N*.N – a.N2 (1)
Onde dN/dt pode ser associado ao número de novos infectados (variação de N) por unidade de tempo (tomada aqui como um dia). É fácil mostrar que o valor máximo da taxa de contaminações acontecerá quando N = N*/2. Na equação de T reconhecemos a equação de uma curva de segundo grau do tipo
[y = a1.x – a2.x2],
mais precisamente, uma parábola. Um ajuste pelo método de mínimos quadrados nos permite estimar o número final de infectados N*; ao atingir metade desse nicho estaremos no máximo de contaminações por dia.
Supondo que o número de óbitos seja uma fração fixa do número de atingidos, o mesmo tipo de equação pode ser usado nos dois casos, tomando dados parciais disponíveis para estimar a quantidade de infeções ou de óbitos finais. Como o número de óbitos tende a ser mais bem avaliado, procuramos nos concentrar aqui nesses dados.
Um problema prático, no caso, é que as políticas de distanciamento social reduzem o tamanho deste nicho. Se essa política é mudada, o nicho também muda de tamanho. Outro problema, no caso do Brasil que tem dimensões continentais, é que a epidemia vai se difundindo aos poucos pelo País e alcança cada município e até cada bairro em diferentes datas. Outro problema prático é a necessidade de uma população relativamente grande para que o tratamento estatístico faça sentido. Nossa escolha foi tratar os dados em três níveis: país região e estados.
Da resolução da equação diferencial dN/dt = a.N.(N-N*) resulta a equação:
F = N/N* = 1/(1+ e(-at-b)) (2)
Onde F é a fração do “nicho” ocupado e a função encontrada é da chamada curva em S, denominada de logística.
Tomando-se o logaritmo neperiano da equação encontra-se
Ln(F/(1-F)) = a.t + b (3)
Essa equação facilita estimar os coeficientes a e b da função logística ajustando uma reta nos valores de Ln(F/(1-F))
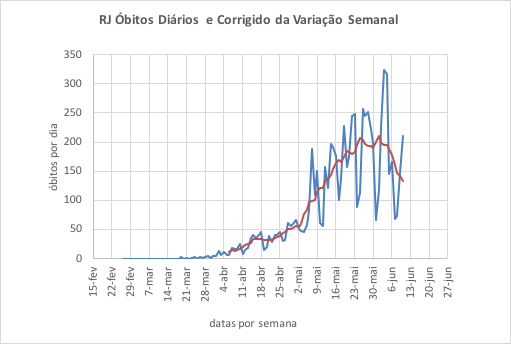
Aplicação da metodologia aos números do Estado do Rio de Janeiro
Os dados, fornecidos pelo MS – Ministério da Saúde, para o Rio de Janeiro são aqui apresentados como exemplo de aplicação da metodologia. Eles se referem ao número de pessoas infectadas e no de óbitos registrados, em consequência da Covid 19. Como já mencionamos, preferimos concentrar a análise nos dados de óbitos, não obstante o retardo implícito das ocorrências e seu registro em relação à data de contaminação.
Ver e baixar arquivo E&E 106 parcial
Aplicação da metodologia aos números do Brasil
A aplicação da metodologia tem suas limitações em um país das dimensões do Brasil onde existem, vários sistemas em ambientes diferentes com uma grande variação de latitude, clima e ocupação do espaço físico.
Ver e baixar arquivo E&E 106 parcial
[1] Cesare Marchetti. Society as a learning system. Technological Forecasting and Social Change, 18:267-282, 1980
[2] https://ecen.com/eee0/eeezero.pdf
[3] http://w.ecen.com/eee45/eee45p/prospeccao_tecnologica.htm
[4] Média quadrática dos desvios relativos
[5] Naturalmente, os últimos três dados ainda estariam sujeitos às variações semanais porque média é centrada (o próprio dia e três anteriores e três posteriores); assim os três últimos dados é feita a correção da “semanalidade” .
[6] O Ministério da Saúde – MS tem divulgados os dados por 100 mil habitantes. No caso, preferimos adotar as mortes por milhão de habitantes que favorecem a comparação diária e não dificultam a acumulada.
[7] J.C. Fisher and R.H. Pry. A simple substitution model of technological change; Technological Forecasting and Social Change, 3:75-88, 1971. https://www.sciencedirect.com/science/article/pii/S0040162571800057